【数学建模】时间序列分析:指数平滑和ARIMA模型
时间序列分析
前言
很多人认为index{ARIMA-ETS equivalences}ARIMA模型相较于指数平滑模型(ETS)更为一般化,这其实是一个较为普遍的错误认识。虽然线性指数平滑模型其实都是 ARIMA 模型的特例,但是非线性的指数平滑模型在 ARIMA 模型中并没有对应的部分。另一方面,也有很多 ARIMA 模型不包含指数平滑的部分。二者还有一个重要区别:所有指数平滑模型都是非平稳的,而有些ARIMA模型是平稳的。
拥有季节性或者非衰减趋势的指数平滑模型拥有两个单位根(即它们需要进行两次差分来实现平稳),其他所有指数平滑模型只有一个单位根(它们需要一次差分来实现平稳)。
ARIMA模型提供了另一种时间序列预测的方法。指数平滑模型(exponential smoothing)和ARIMA模型是应用最为广泛的两种时间序列预测方法,基于对这两种预测方法的拓展,很多其他的预测方法得以诞生。与指数平滑模型针对于数据中的趋势(trend)和季节性(seasonality)不同,ARIMA模型旨在描绘数据的自回归性(autocorrelations)。
在引入ARIMA模型之前,我们需要先讨论平稳性(stationarity)和差分时间序列(differencing time series)的相关知识。
时期序列和时点序列的概念
时期序列可加,时点不可加
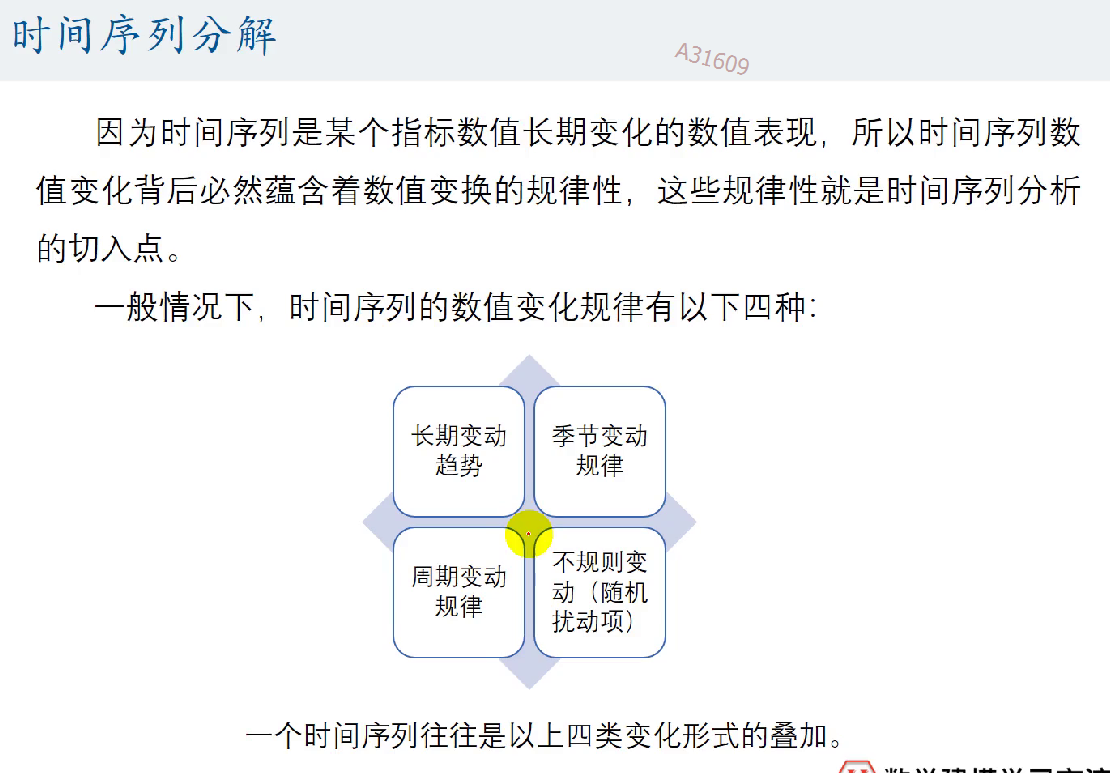
时间序列分解
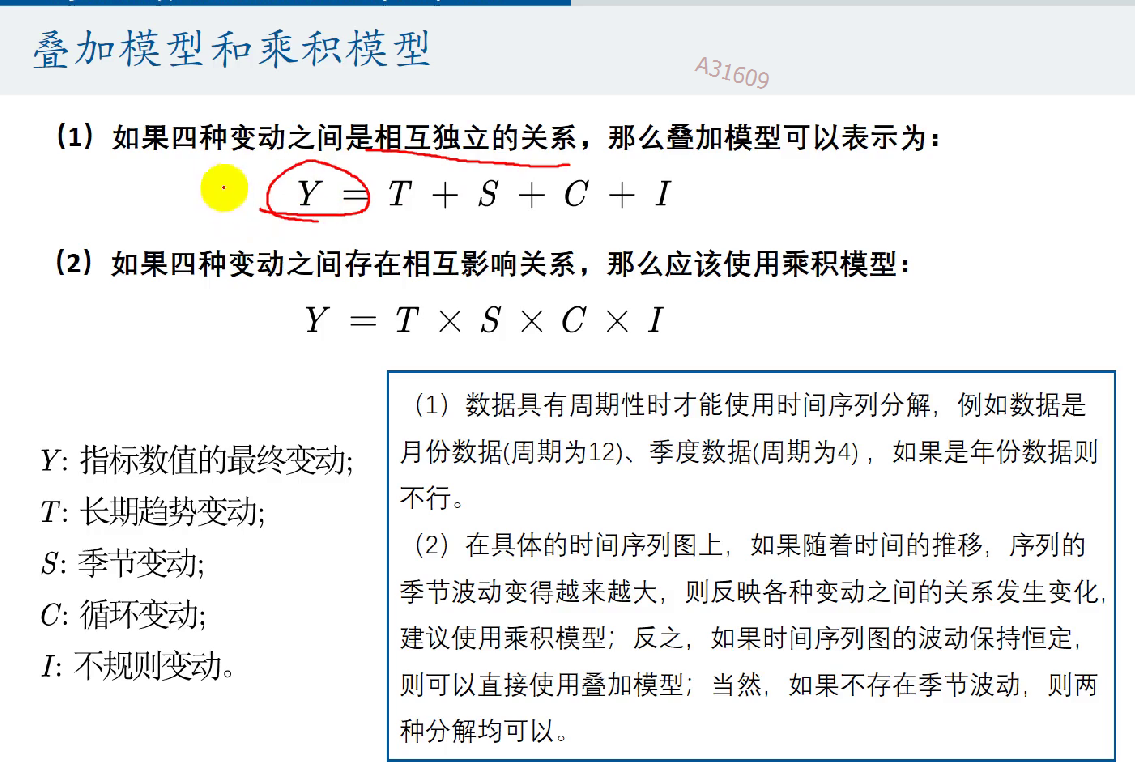
叠加模型和乘积模型
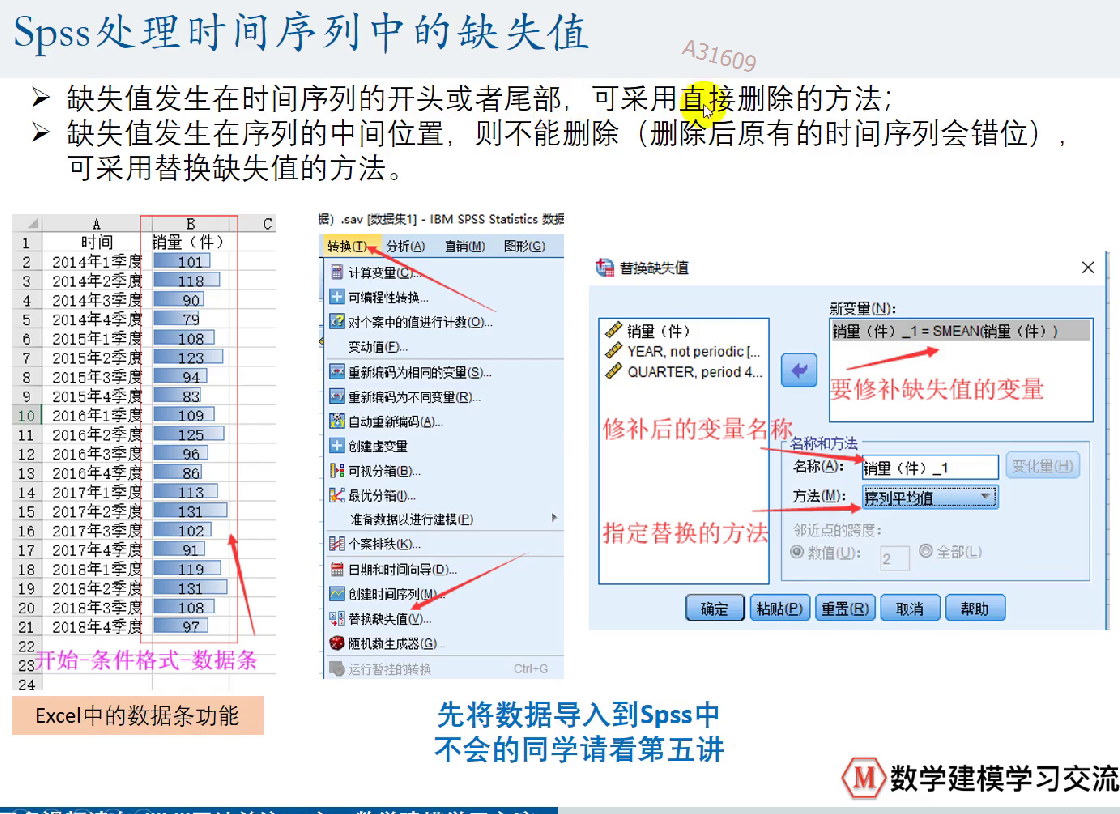
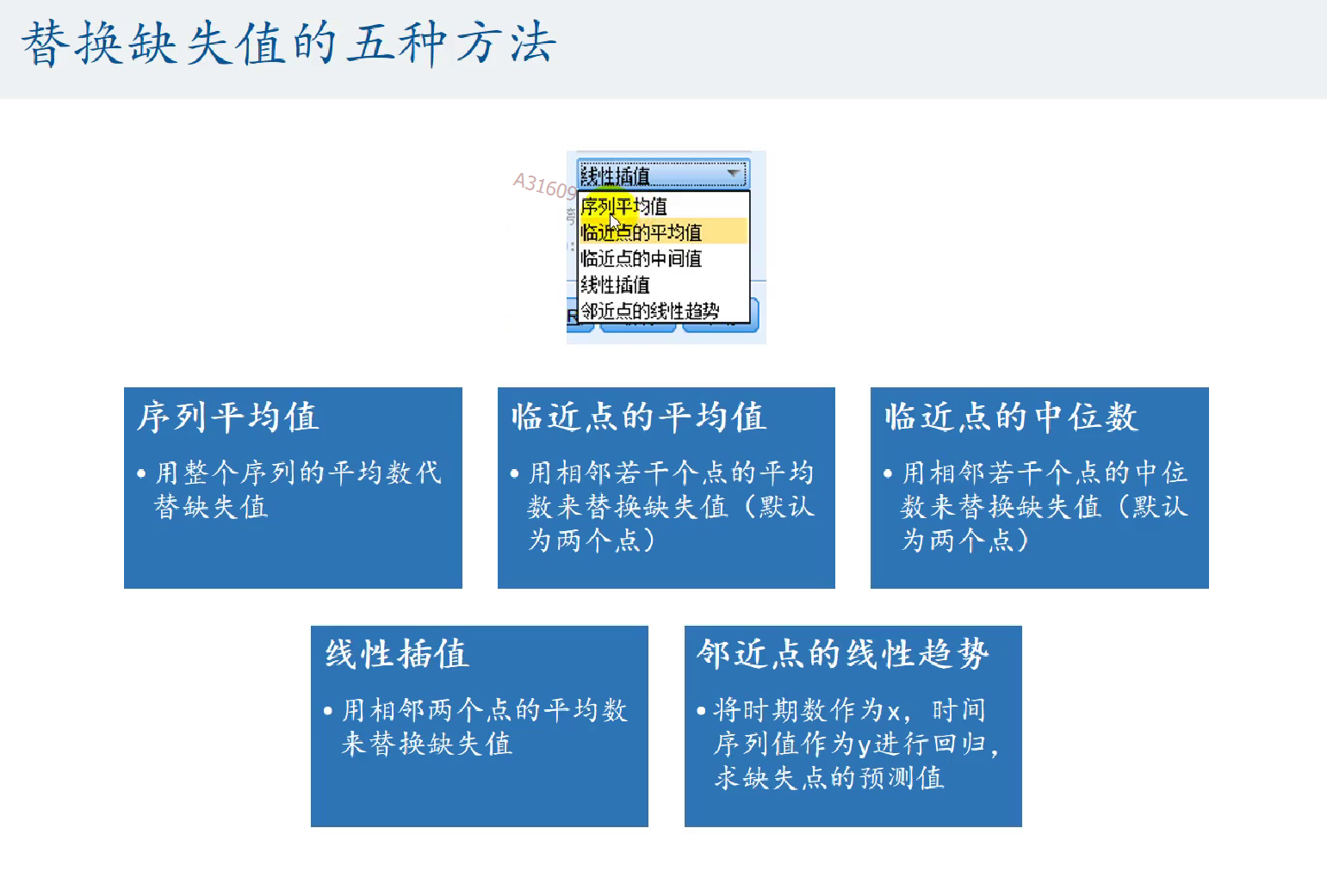
如何处理缺失值
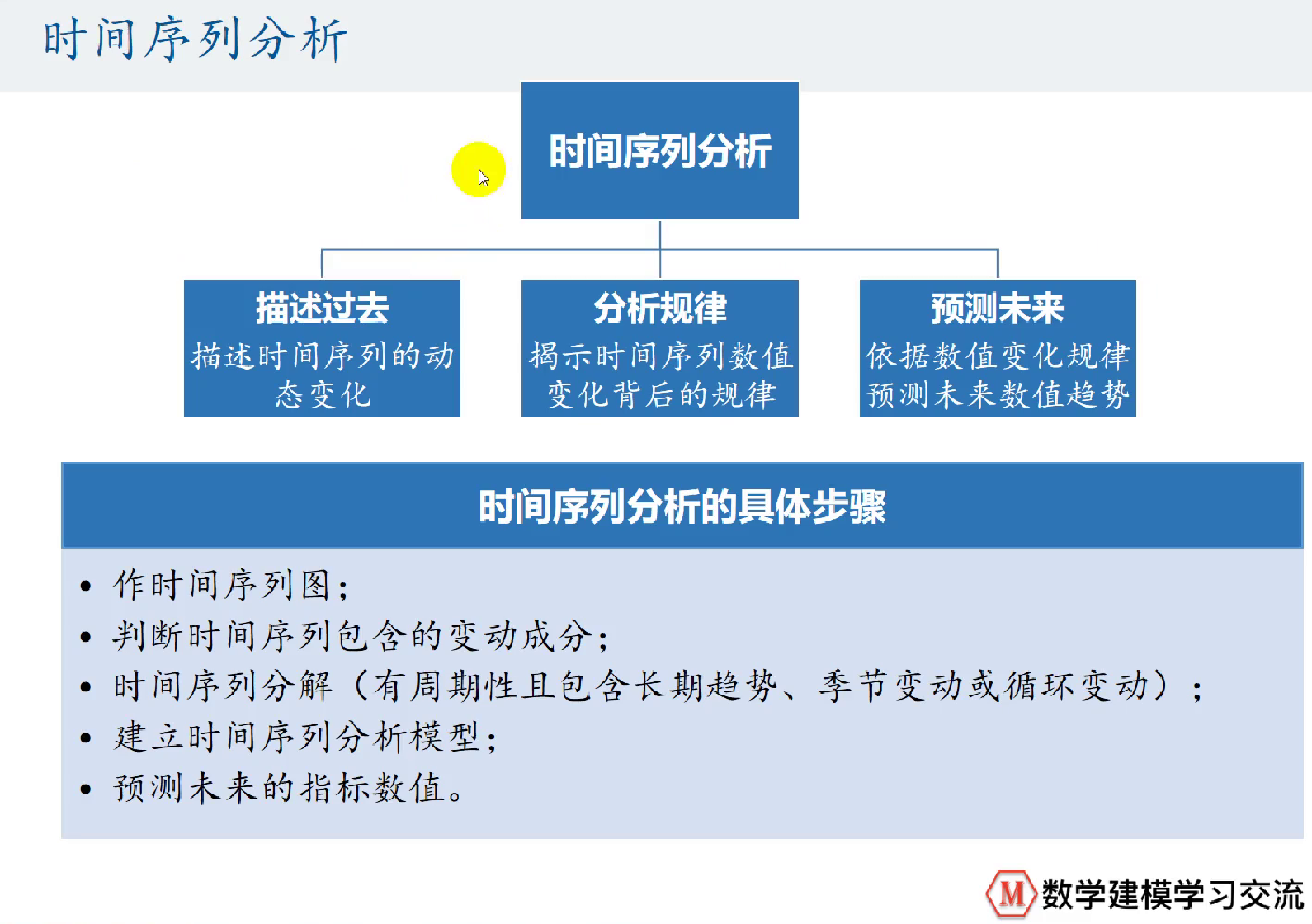
具体步骤:
周期要小于一年
指数回归模型:
一元时间序列分析模型
为了引出ARIMA模型
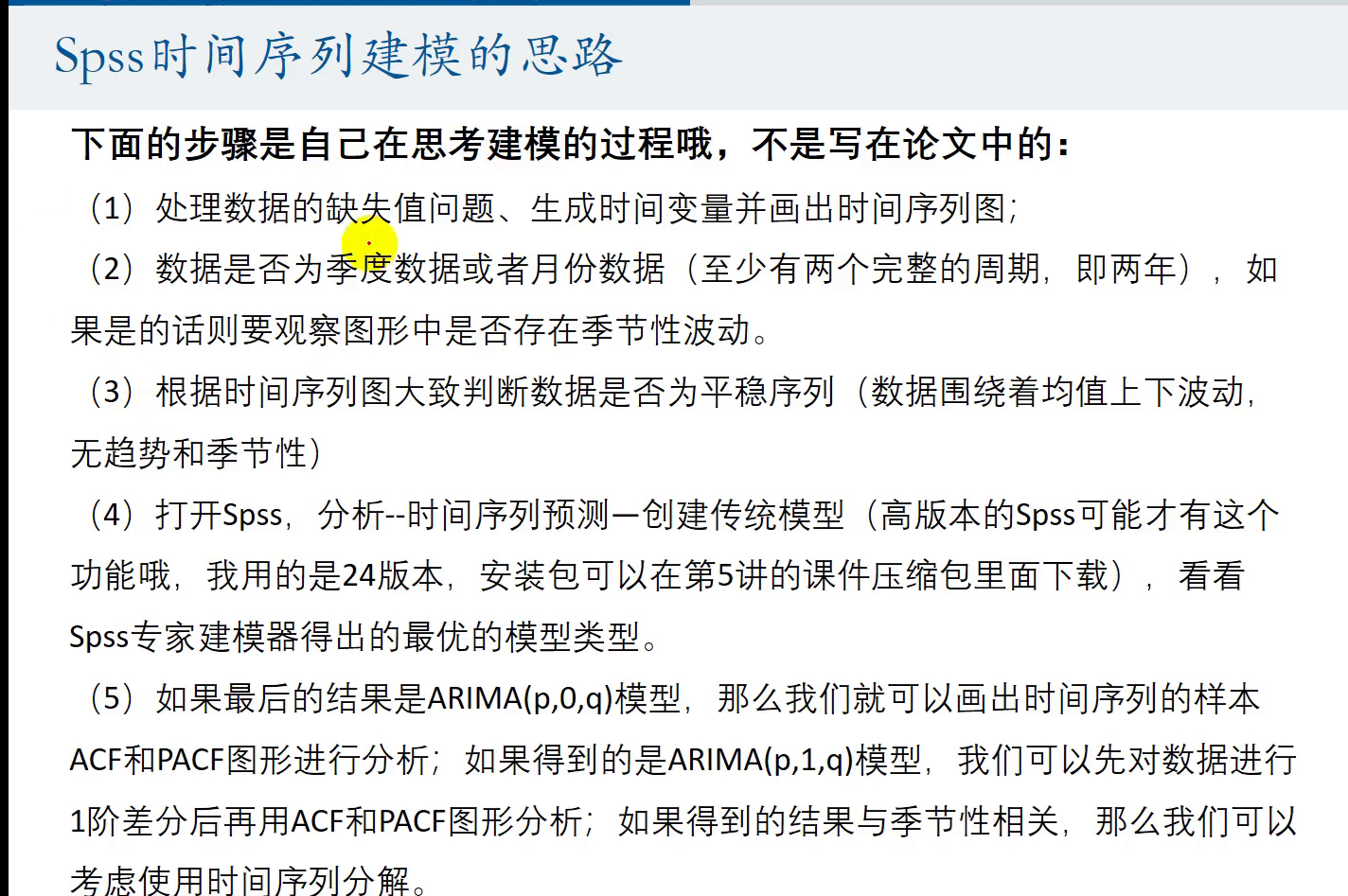
建模过程:
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Naylen's Blog!
评论