排队论

这篇博客写的太好了，我就偷懒一点：

数学建模之排队论

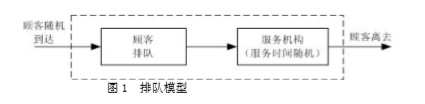
排队论的一般模型：

这里要注意，分析清除排队论种的排队顾客具体是谁。19年国赛C的顾客就是汽车司机，不是乘客。

排队系统的组成和特征

一般的排队过程都由输入过程、排队规则、服务过程三部分组成

排队规则

排队规则指到达排队系统的顾客按怎样的规则排队等待，可分为损失制，等待制和混合制三种.

损失制（消失制）。当顾客到达时，所有的服务台均被占用，顾客随即离去。
等待制。当顾客到达时，所有的服务台均被占用，顾客就排队等待，直到接受完服务才离去。例如出故障的机器排队等待维修就是这种情况。

排队方式还分为单列、多列和循环队列。

服务过程

先到先服务 FCFS
后到先服务 LCFS （很少见）

排队模型的符号表示（直接复制了

排队模型用六个符号表示，在符号之间用斜线隔开，即 X/Y/Z/A/B/C 。第一个符号 X 表示顾客到达流或顾客到达间隔时间的分布；第二个符号Y 表示服务时间的分布；第三个符号Z 表示服务台数目；第四个符号 A是系统容量限制；第五个符号B 是顾客源数目；第六个符号C 是服务规则，如先到先服务 FCFS，后到先服务 LCFS 等。并约定，如略去后三项，即指X/Y/Z/∞/∞/FCFS的情形。我们只讨论先到先服务 FCFS 的情形，所以略去第六项。
表示顾客到达间隔时间和服务时间的分布的约定符号为：
M —指数分布（M 是 Markov 的字头，因为指数分布具有无记忆性，即 Markov 性）；
D—确定型（Deterministic）；
Ek —k 阶爱尔朗(Erlang)分布；
G —一般（general）服务时间的分布；
GI —一般相互独立（General Independent）的时间间隔的分布。
例如，M/M/1表示相继到达间隔时间为指数分布、服务时间为指数分布、单服务台、等待制系统。
D/M/c/表示确定的到达时间、服务时间为指数分布、c个平行服务台（但顾客是一队）的模型。